e c a b o u n d a r i e s
A challenge with running eca’s is the impossibility of representing a row with an infinite set of cells. In practical terms, this means limiting the number of cells in a row.
Pure Patterns
A pure pattern is one where the limits have no impact on the pattern generated. In practical terms, this means specifying the number of rows and the size of the seed row so the sides don't affect the pattern. For a 3-cell block automaton, specify the number of rows then take that number, multiply by 2, and add the number of cells in the seed for the minimum size of the seed row. So for a pattern with a single seed and 15 rows, the width would be (15 x 2) +1 or 31 cells.
Note: in many of the charts the Pure patterns are much narrower than they are deep. The initial specs for these rules were set to ensure a pure pattern and then the image was cropped.
There is “pureness” in every pattern run depending on the specification of the seed row. If the boundary condition is periodic or mirror (see below), the pure area runs from the row where the pattern meets the end of the row and then triangles down.
If the boundary condition is arbitrary or the seed row is the full width of the pattern, the pure area is a triangle running down from the edges of the pattern to the center of the seed.
See the Eca Pure Areas chart for some examples.
Boundaries
The trick becomes how to apply the rule at the end of the row. As shown below, in a single seed three-cell block eca, when the rule gets to the end of the row, the target cell (either A or Z) only has one neighbor.
| A | B | S | Y | Z | ||||
| 0 | 0 | 0 | 1 | 2 | 4 | 0 | 0 | 0 |
One alternative is to recognize that the state of the last cells in the row can’t be resolved and they become null, neither active or passive. The new row will therefore shrink by two cells and subsequent rows will shrink until there are no cells left in the row and the pattern generated is an inverted triangle under the seed. In this diagram, the null cells are colored grey (active or passive state is immaterial to this problem):
| A | B | S | Y | Z | ||||
| ?? | 0 | 0 | 1 | 2 | 4 | 0 | 0 | ?? |
| 0 | 0 | 0 | 1 | 2 | 4 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 2 | 4 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 2 | 4 | 0 | 0 | 0 |
One resolution is to visualize the row wrapped around a cylinder. That way, the end cells have a neighbor to complete the three-cell block. The light red cell in the illustration below, the left end cell, now can be determined by the block Z-A-B:
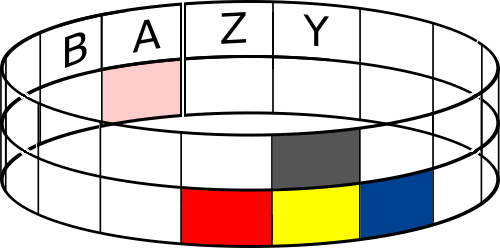
Unwrap the cylinder, keep the wrap around end cell, and the time step now has an extra cell at each end. As shown below, the seed row is padded with the two wrap around cells, shown in light blue. With this padding, there is sufficient information to determine the rule affecting the two end cells on the first row. The end of each subsequent row is padded in the same way.
| Z | A | B | S | Y | Z | A | ||||
| A | 0 | 0 | 1 | 2 | 4 | 0 | 0 | A |
The trick is determining what to use to pad the rows. This depends on the purpose of the pattern and what wants to be shown.
01. Periodic or Wrap Around: This is the standard method, shown the in illustrations above, where the value of the last cell on the right is used to pad the left side, and the value of the last cell on the left pads the right side. The effect is like generating the patterns on the surface of a tube and provides a result that is as close to pure as possible, particularly with large arrays.
02. Mirror or Duplicative: This is the opposite of the Periodic. The value of the last cell on the right is used to pad the right side, and the value of the last cell on the left pads the left side. This also results in the pattern continuing within the confines of the boundary without a great deal of perturbation.
| A | A | B | S | Y | Z | Z | ||||
| A | 0 | 0 | 1 | 2 | 4 | 0 | 0 | A |
03. Arbitrary:
- Passive: the ends are padded with passive cells
- Active: the ends are padded with active cells
- Other: including random padding
Bounding the generation of a rule does have consequences because the number of possible row patterns displayed. The general equation to calculate the number of possible patterns for a row with n number of cells in a row is 2^n. If:
- n = 11, patterns = 2,048
- n = 21, patterns = 2,097,152
- n = 31, patterns = 2,147,483,648
- n = 51, patterns = 2,251,799,814,###,### or more than 2 quadrillion
Observation indicates that boundary conditions can distort the patterns. The periodic boundary appears to retain the essence of the pattern as does the mirrored boundary. The active and passive boundaries have a greater distorting affect.
There are cases where boundaries appear to have no effect, particularly those patterns with a vertical orientation. Some patterns are more distorted than others.
A chart of rules run using a single seed under various boundary conditions and widths between boundaries.
Another one using multi-seed conditions.